Disciplina: Matemática, Apontamentos nas Disciplinas básicas (gerais) e essenciais
Apontamentos do Tema: Geometria
Geometria
A geometria é uma área da matemática que estuda as formas geométricas desde comprimento, área e volume. O vocábulo geometria corresponde a união dos termos “geo” (terra) e “metron” (medir), ou seja, a “medida de terra”.
A Geometria é dividida em três categorias:
- Geometria Analítica
- Geometria Plana
- Geometria Espacial
Assim, a geometria analítica, também chamada de geometria cartesiana, une conceitos de álgebra e geometria através dos sistemas de coordenadas. Os conceitos mais utilizados são o ponto e a reta.
Enquanto a geometria plana ou euclidiana reúne os estudos sobre as figuras planas, ou seja, as que não apresentam volume, a geometria espacial estuda as figuras geométricas que possuem volume e mais de uma dimensão.
Comentários:
Compilado por Formador: Jose Bernardo Muchanga
Seno, Cosseno e Tangente
Seno, Cosseno e Tangente de um ângulo são relações entre os lados de um triângulo retângulo. Essas relações são chamadas de razões trigonométricas, pois resultam da divisão entre as medidas dos seus lados.
O triângulo retângulo é aquele que apresenta um ângulo interno reto (igual a 90º). O lado oposto ao ângulo de 90º é chamado de hipotenusa e os outros dois lados são chamados de catetos.
Os valores do seno, do cosseno e da tangente são calculados em relação a um determinado ângulo agudo do triângulo retângulo.
De acordo com a posição dos catetos em relação ao ângulo, ele pode ser oposto ou adjacente, conforme imagem abaixo:
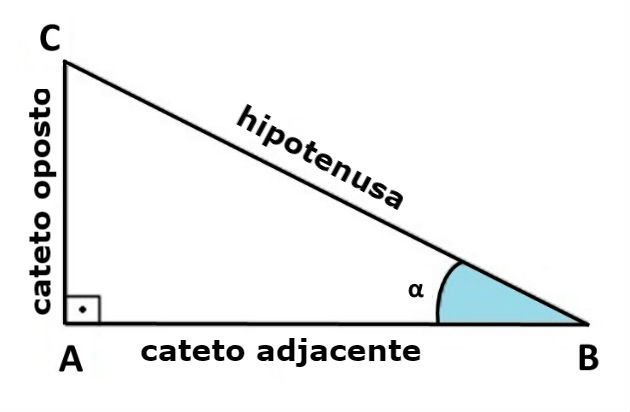
Seno (Sen )
É a razão entre a medida do cateto oposto ao ângulo agudo e a medida da hipotenusa de um triângulo retângulo. Essa relação é calculada através da fórmula:
Lê-se cateto oposto sobre a hipotenusa.
Veja também: Lei dos Senos
Ainda com dúvidas? Pergunta ao Ajudante IA do Toda Matéria
Palavras: 0/900
Utilizações: 0/5
Resolver
Insira ou cole sua questão (Ctrl + V). Depois, aperte Resolver.
Colar texto
ou
Inserir imagem
Cosseno (Cos )
É a razão entre a medida do cateto adjacente ao ângulo agudo e a medida da hipotenusa de um triângulo retângulo. Essa relação é calculada através da fórmula:
Lê-se cateto adjacente sobre a hipotenusa.
Veja também: Lei dos Cossenos
Tangente (Tg )
É a razão entre a medida do cateto oposto e a medida do cateto adjacente ao ângulo agudo de um triângulo retângulo. Essa relação é calculada através da fórmula:
Lê-se cateto oposto sobre cateto adjacente.
Veja também: Trigonometria no Triângulo Retângulo
Tabela Trigonométrica
Na tabela trigonométrica consta o valor de cada razão trigonométrica para os ângulos de 1º a 90º.
Os ângulos de 30º, 45º e 60º são os mais usados nos cálculos e por isso, eles são chamados de ângulos notáveis.
| Relações Trigonométricas | 30° | 45° | 60° |
|---|---|---|---|
| Seno | 1/2 | √2/2 | √3/2 |
| Cosseno | √3/2 | √2/2 | 1/2 |
| Tangente | √3/3 | 1 | √3 |
Veja também: Relações Métricas no Triângulo Retângulo
Como Calcular as Razões Trigonométricas?
Para compreender melhor a aplicação das fórmulas, confira abaixo dois exemplos:
1) Encontre os valores do seno, cosseno e tangente do ângulo do triângulo abaixo.
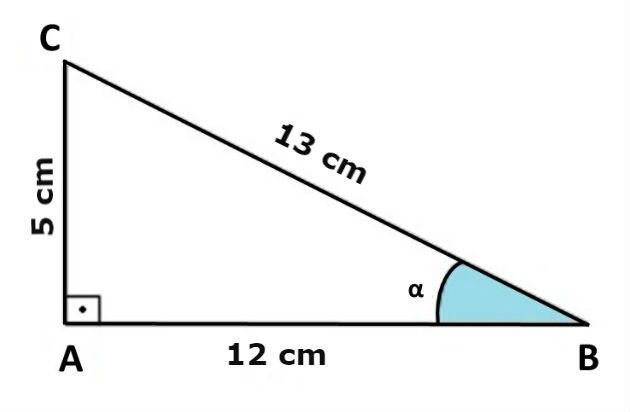
Solução
Para encontrar os valores do seno, cosseno e tangente, devemos substituir a medida de cada lado do triângulo nas respectivas fórmulas.
Observando a imagem, identificamos que o cateto oposto mede 5 cm, o cateto adjacente mede 12 cm e a medida da hipotenusa é igual a 13 cm. Assim, temos:
Veja também: Relações Trigonométricas
2) Determine o valor de x na figura abaixo.
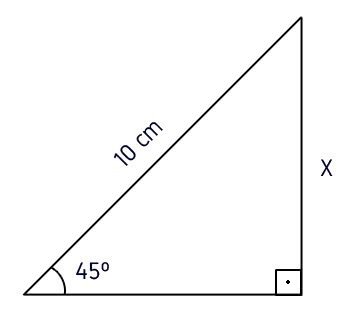
Observe que temos a medida da hipotenusa (10 cm) e queremos descobrir a medida de x, que é o cateto oposto ao ângulo de 45º. Desta forma, aplicaremos a fórmula do seno.
De acordo com a tabela trigonométrica, o valor do seno de 45.º é aproximadamente igual a 0,7071. Assim:
Portanto, o lado x mede 7,071 cm.

Veja também: Razões Trigonométricas
Exercícios de Vestibular
1. (UFPI) Um avião decola, percorrendo uma trajetória retilínea, formando com o solo, um ângulo de 30º (suponha que a região sobrevoada pelo avião seja plana). Depois de percorrer 1 000 metros, qual a altura atingida pelo avião?
Ver Resposta
2.(Cefet-MG) O triângulo ABC é retângulo em e os segmentos são perpendiculares.
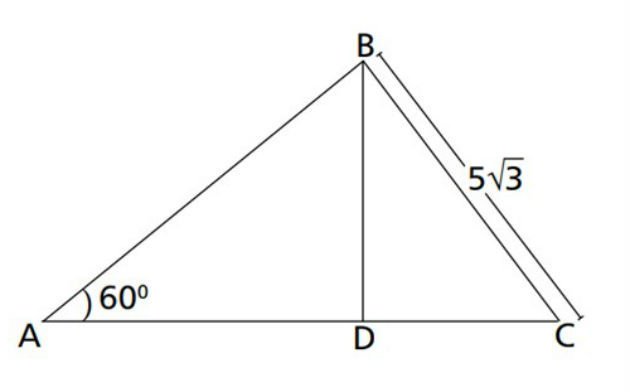
Assim, a medida do segmento vale
Comentários:
Compilado por Formador: Jose Bernardo Muchanga
Sobre JBM
Esta página foi projetada por JBM para facilitar ao usuário a busca parcial e completa dos conteúdos de várias disciplinas, enriquecendo assim seus estudos.
Gerar pedf desse apontamento inicio


