O Teorema de Pitágoras relaciona o comprimento dos lados do triângulo retângulo. Essa figura geométrica é formada por um ângulo interno de 90°, chamado de ângulo reto.

É usado para determinar a medida desconhecida de um lado, uma vez conhecidas as medidas dos outros dois lados.

O enunciado desse teorema é:

“A hipotenusa ao quadrado é igual a soma dos quadrados dos catetos.”

Em forma de equação, a fórmula do Teorema de Pitágoras é:

 

Sendo,

a: hipotenusa
b: cateto
c: cateto

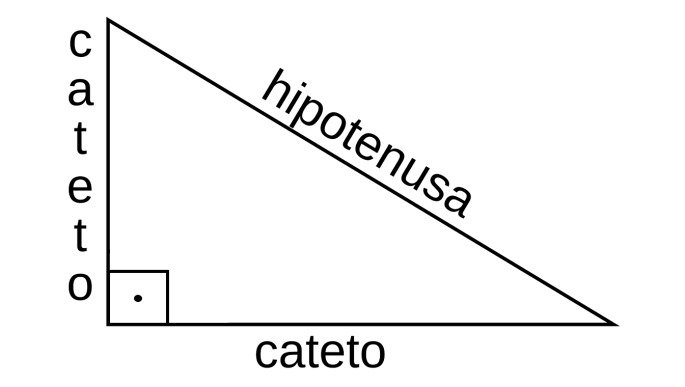
Triângulo retângulo. Os catetos formam 90º.

Como usar o Teorema de Pitágoras

Veja a seguir exemplos do uso do teorema de Pitágoras para determinar uma medida desconhecida do triângulo.

Exemplo 1: como calcular a medida da hipotenusa?

Se um triângulo retângulo apresenta 3 cm e 4 cm como medidas dos catetos, qual a hipotenusa desse triângulo?

 

Portanto, a hipotenusa mede 5 cm.

Exemplo 2: como calcular a medida de um dos catetos?

Determine a medida de um cateto que faz parte de um triângulo retângulo, cuja hipotenusa é 20 cm e o outro cateto mede 16 cm.

 

Portanto, as medidas dos catetos do triângulo são 12 cm e 16 cm.

Exemplo 3: como comprovar se um triângulo é retângulo?

Um triângulo apresenta os lados com medidas 5 cm, 12 cm e 13 cm. Como saber se é um triângulo retângulo?

Para provar que um triângulo retângulo é verdadeiro as medidas dos seus lados devem obedecer ao Teorema de Pitágoras.

 

Como as medidas dadas satisfazem o teorema de Pitágoras, ou seja, o quadrado da hipotenusa é igual a soma do quadrado dos catetos, então podemos dizer que o triângulo é retângulo.

Ainda com dúvidas? Pergunta ao Ajudante IA do Toda Matéria

Palavras: 0/900

Utilizações: 0/5

Resolver

Insira ou cole sua questão (Ctrl + V). Depois, aperte Resolver.

Colar texto

ou

Inserir imagem

Exercícios comentados sobre o Teorema de Pitágoras

Questão 1

(PUC) A soma dos quadrados dos três lados de um triângulo retângulo é igual a 32. Quanto mede a hipotenusa do triângulo?

 

Remover anúncios

a) 3
b) 4
c) 5
d) 6

Alternativa correta: b) 4.

Ver Resposta

Questão 2

(Enem)

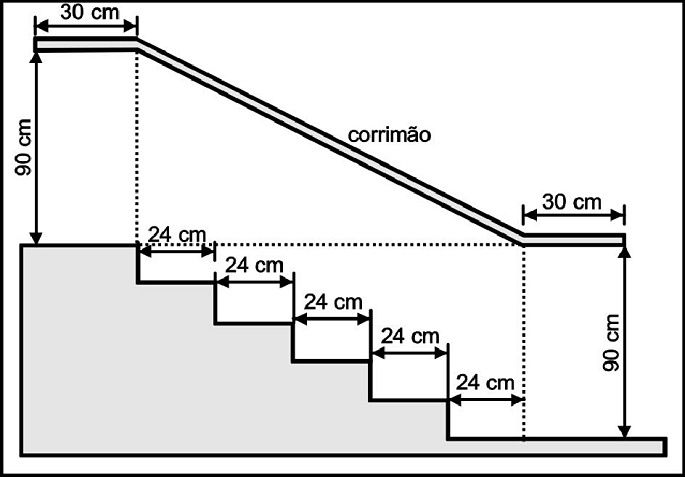
Na figura acima, que representa o projeto de uma escada com 5 degraus de mesma altura, o comprimento total do corrimão é igual a:

a) 1,9m
b) 2,1m
c) 2,0m
d) 1,8m
e) 2,2m

 

Remover anúncios

Ver Resposta

Questão 3

(UERJ) Millôr Fernandes, em uma bela homenagem à Matemática, escreveu um poema do qual extraímos o fragmento abaixo:

Às folhas tantas de um livro de Matemática,
um Quociente apaixonou-se um dia doidamente
por uma Incógnita.
Olhou-a com seu olhar inumerável
e viu-a do ápice à base: uma figura ímpar;
olhos rombóides, boca trapezóide,
corpo retangular, seios esferóides.
Fez da sua uma vida paralela à dela,
até que se encontraram no Infinito.
“Quem és tu?” – indagou ele em ânsia radical.
“Sou a soma dos quadrados dos catetos.
Mas pode me chamar de hipotenusa.”

(Millôr Fernandes. Trinta Anos de Mim Mesmo.)

A Incógnita se enganou ao dizer quem era. Para atender ao Teorema de Pitágoras, deveria dar a seguinte

a) “Sou o quadrado da soma dos catetos. Mas pode me chamar de quadrado da hipotenusa.”
b) “Sou a soma dos catetos. Mas pode me chamar de hipotenusa.”
c) “Sou o quadrado da soma dos catetos. Mas pode me chamar de hipotenusa.”
d) “Sou a soma dos quadrados dos catetos. Mas pode me chamar de quadrado da hipotenusa.”

Ver Resposta

Pratique Exercícios sobre Teorema de Pitágoras.

Triângulo Pitagórico

Quando as medidas dos lados de um triângulo retângulo são números inteiros positivos, o triângulo é chamado de triângulo pitagórico.

Neste caso, os catetos e a hipotenusa são denominados de “terno pitagórico” ou “trio pitagórico”. Para verificar se três números formam um trio pitagórico, usamos a relação a2 = b2 + c2.

O mais conhecido trio pitagórico é representado pelos números: 3, 4, 5. Sendo a hipotenusa igual a 5, o cateto maior igual a 4 e o cateto menor igual a 3.

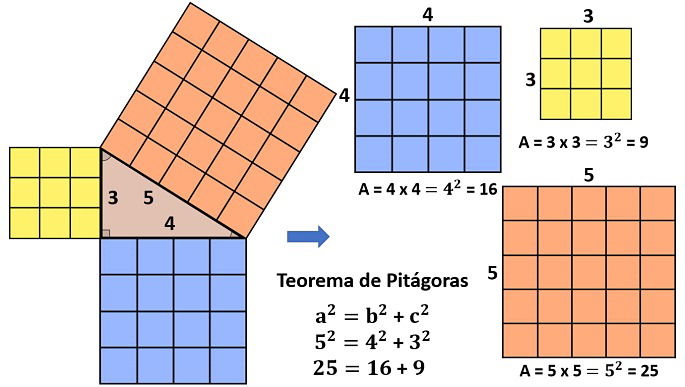
Observe que a área dos quadrados desenhados em cada lado do triângulo relacionam-se tal como o teorema de Pitágoras: a área do quadrado no lado maior corresponde à soma das áreas dos outros dois quadrados.

É interessante notar que, os múltiplos desses números também formam um terno pitagórico. Por exemplo, se multiplicarmos por 3 o trio 3, 4 e 5, obtemos os números 9, 12 e 15 que também formam um terno pitagórico.

Além do terno 3, 4 e 5, existe uma infinidade de outros ternos. Como exemplo, podemos citar:

• 5, 12 e 13
• 7, 24, 25
• 20, 21 e 29
• 12, 35 e 37

Veja mais sobre triângulo retângulo.

Quem foi Pitágoras?

Segundo a história Pitágoras de Samos (570 a.C. - 495 a.C.) foi um filósofo e matemático grego que fundou a Escola Pitagórica, localizada no sul da Itália. Também chamada de Sociedade Pitagórica, incluía estudos de Matemática, Astronomia e Música.

Embora as relações métricas do triângulo retângulo já fossem conhecidas pelos babilônicos, que viveram muito antes de Pitágoras, acredita-se que a primeira demonstração que esse teorema se aplicava a qualquer triângulo retângulo tenha sido feita por Pitágoras.

O Teorema de Pitágoras é um dos teoremas mais conhecidos, importantes e utilizados na matemática. Ele é imprescindível na resolução de problemas da geometria analítica, geometria plana, geometria espacial e trigonometria.

Além do teorema, outras importantes contribuições da Sociedade Pitagórica para a Matemática foram:

• Descoberta dos números irracionais;
• Propriedades dos números inteiros;
• MMC e MDC.

Demonstrações do Teorema de Pitágoras

Existem diversas formas de provar o teorema de Pitágoras. Por exemplo, o livro The Pythagorean Proposition, publicado em 1927, apresentava 230 formas de demonstrá-lo e outra edição, lançada em 1940, aumentou para 370 demonstrações.

Assista o vídeo a seguir e confira algumas demonstrações do Teorema de Pitágoras.

Saiba mais sobre:

• Triângulo: tudo sobre este polígono
• Triângulo Isósceles
• Relações Métricas no Triângulo Retângulo
• Exercícios sobre Teorema de Tales
• Seno, Cosseno e Tangente
• Teorema de Tales
• Matemática no Enem
• Hipotenusa: como calcular sua medida
• Trigonometria no Triângulo Retângulo
• Exercícios de Trigonometria
• Fórmulas de Matemática