As relações métricas relacionam as medidas dos elementos de um triângulo retângulo (triângulo com um ângulo de 90º).

Os elementos de um triângulo retângulo estão apresentados abaixo:

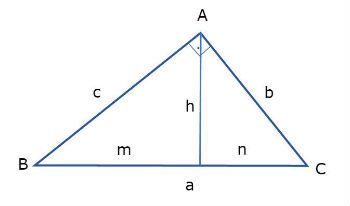
Sendo:

a: medida da hipotenusa (lado oposto ao ângulo de 90º)
b: cateto
c: cateto
h: altura relativa à hipotenusa
m: projeção do cateto c sobre a hipotenusa
n: projeção do cateto b sobre a hipotenusa

Semelhança e relações métricas

Para encontrar as relações métricas, utilizaremos semelhança de triângulos. Considere os triângulos semelhantes ABC, HBA e HAC, representados nas imagens:

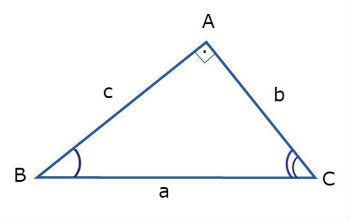
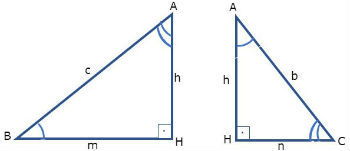
Como os triângulos ABC e HBA são semelhantes (), temos as seguintes proporções:

Remover anúncios

Usando que  encontramos a proporção:

Da semelhança entre os triângulos HBA e HAC encontramos a proporção:

Temos ainda que a soma das projeções m e n é igual a hipotenusa, ou seja:

Teorema de Pitágoras

A mais importante das relações métricas é o Teorema de Pitágoras. Podemos demonstrar o teorema usando a soma de duas relações encontradas anteriormente.

Vamos somar a relação b2 = a . n com c2 = a . m, conforme mostrado abaixo:

Como a = m + n, substituindo na expressão anterior, temos:

Assim, o Teorema de Pitágoras pode ser enunciado como:

A hipotenusa ao quadrado é igual a soma dos quadrados dos catetos.

Exemplos

1) Encontre o valor de x e de y na figura abaixo:

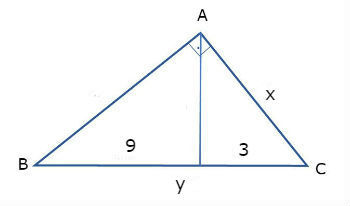
Primeiro calcularemos o valor da hipotenusa, que na figura está representado por y.
Usando a relação: a = m + n
y = 9 + 3
y = 12

Para encontrar o valor de x, usaremos a relação b2 = a.n, assim:
x2 = 12 . 3 = 36

2) A medida da altura relativa à hipotenusa de um triângulo retângulo é 12 cm e uma das projeções mede 9 cm. Calcular a medida dos catetos desse triângulo.

Remover anúncios

Primeiro vamos encontrar o valor da outra projeção usando a relação: h2 = m . n

Vamos encontrar o valor da hipotenusa, usando a relação a = m + n
a = 16 + 9 = 25
Agora é possível calcular o valor dos catetos usando as relações b2 = a . n e c2 = a . m

Ainda com dúvidas? Pergunta ao Ajudante IA do Toda Matéria

Palavras: 0/900

Utilizações: 0/5

Resolver

Insira ou cole sua questão (Ctrl + V). Depois, aperte Resolver.

Colar texto

ou

Inserir imagem

Fórmulas

Na tabela abaixo, reunimos as relações métricas no triângulo retângulo.

Para saber mais, leia também:

• Trigonometria no Triângulo Retângulo
• Exercícios sobre Semelhança de Triângulos
• Exercícios de trigonometria no triângulo retângulo
• Exercícios sobre Teorema de Tales
• Soma dos ângulos internos de um triângulo
• Exercícios de Trigonometria
• Triângulo Retângulo
• Teorema de Tales
• Exercícios sobre Teorema de Pitágoras
• Razões Trigonométricas
• Seno, Cosseno e Tangente
• Exercícios de seno, cosseno e tangente
• Exercícios sobre razões trigonométricas
• Relações Trigonométricas
• Identidades trigonométricas
• Fórmulas de Matemática

Exercícios Resolvidos

1) Num triângulo retângulo, a hipotenusa mede 10 cm e um dos catetos mede 8 cm. Nessas condições, determine:

a) a medida da altura relativa à hipotenusa
b) a área do triângulo