Disciplina: Matemática, Apontamentos nas Disciplinas básicas (gerais) e essenciais
Apontamentos do Tema: Lei dos Senos
Lei dos Senos
A Lei dos Senos determina que num triângulo qualquer, a relação do seno de um ângulo é sempre proporcional à medida do lado oposto a esse ângulo.
Esse teorema demonstra que num mesmo triângulo a razão entre o valor de um lado e o seno de seu ângulo oposto será sempre constante.
Assim, para um triângulo ABC de lados a, b, c, a Lei dos Senos admite as seguintes relações:
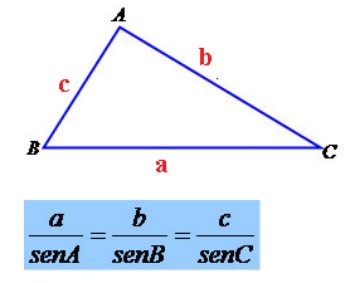
Representação da Lei dos Senos no triângulo.
Exemplo
Para compreender melhor, vamos calcular a medida dos lados AB e BC desse triângulo, em função da medida b do lado AC.
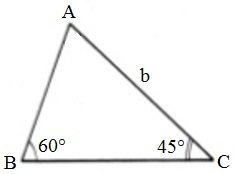
Pela lei dos senos, podemos estabelecer a seguinte relação:

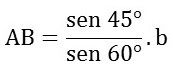
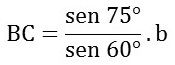
Logo, AB = 0,816b e BC = 1,115b.
Obs: Os valores dos senos foram consultados na tabela das razões trigonométricas. Nela, podemos encontrar os valores dos ângulos de 1º a 90º de cada função trigonométrica (seno, cosseno e tangente).
Os ângulos de 30º, 45º e 60º são os mais usados nos cálculos de trigonometria. Por isso, eles são chamados de ângulos notáveis. Confira abaixo um quadro com os valores:
| Relações Trigonométricas | 30° | 45° | 60° |
|---|---|---|---|
| Seno | 1/2 | √2/2 | √3/2 |
| Cosseno | √3/2 | √2/2 | 1/2 |
| Tangente | √3/3 | 1 | √3 |
Ainda com dúvidas? Pergunta ao Ajudante IA do Toda Matéria
Palavras: 0/900
Utilizações: 0/5
Resolver
Insira ou cole sua questão (Ctrl + V). Depois, aperte Resolver.
Colar texto
ou
Inserir imagem
Aplicação da Lei dos Senos
Utilizamos a Lei dos Senos nos triângulos acutângulos, onde os ângulos internos são menores que 90º (agudos); ou nos triângulos obtusângulos, que apresentam ângulos internos maiores que 90º (obtusos). Nesses casos, também é possível utilizar a Lei dos Cossenos.
O objetivo principal da utilização da Lei dos Senos ou Cossenos é de descobrir as medidas dos lados de um triângulo e ainda, de seus ângulos.

Representação de triângulos segundo seus ângulos internos
E a Lei dos Senos no Triângulo Retângulo?
Como mencionado acima, a Lei dos Senos é utilizada nos triângulos acutângulos e obtusângulos.
Já nos triângulos retângulos, formados por um ângulo interno de 90º (reto), utilizamos o Teorema de Pitágoras e as relações entre seus lados: cateto oposto, adjacente e hipotenusa.
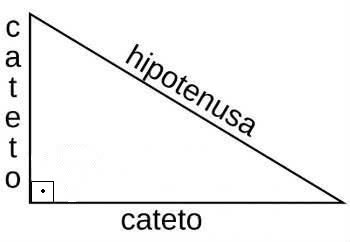
Representação do triângulo retângulo e seus lados
Esse teorema possui o seguinte enunciado: "a soma dos quadrados de seus catetos corresponde ao quadrado de sua hipotenusa". Sua fórmula é expressa:
h2 = ca2 + co2
Assim, quando temos um triângulo retângulo, o seno será à razão entre o comprimento do cateto oposto e o comprimento da hipotenusa:
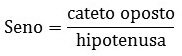
Lê-se cateto oposto sobre a hipotenusa.
Já o cosseno, corresponde à proporção entre o comprimento do cateto adjacente e o comprimento da hipotenusa, representado pela expressão:
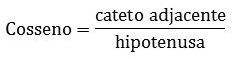
Lê-se cateto adjacente sobre a hipotenusa.
Exercícios de Vestibular
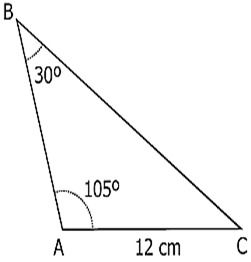
1.(UFPB) A prefeitura de certa cidade vai construir, sobre um rio que corta essa cidade, uma ponte que deve ser reta e ligar dois pontos, A e B, localizados nas margens opostas do rio. Para medir a distância entre esses pontos, um topógrafo localizou um terceiro ponto, C, distante 200 m do ponto A e na mesma margem do rio onde se encontra o ponto A. Usando um teodolito (instrumento de precisão para medir ângulos horizontais e ângulos verticais, muito empregado em trabalhos topográficos), o topógrafo observou que os ângulos mediam, respectivamente, 30º e 105º, conforme ilustrado na figura a seguir.
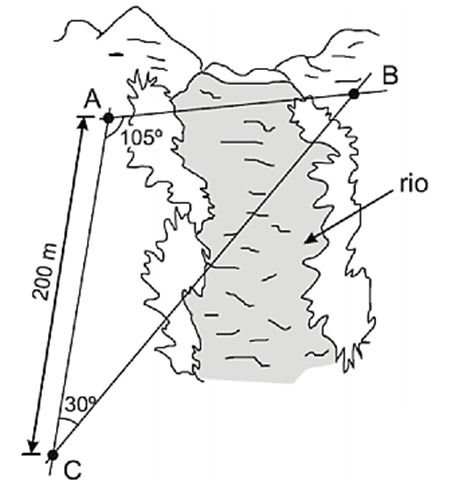
Com base nessas informações, é correto afirmar que a distância, em metros, do ponto A ao ponto B é de:
Ver Resposta
2. (Mackenzie – SP) Três ilhas A, B e C aparecem num mapa em escala 1:10000, como na figura. Das alternativas, a que melhor aproxima a distância entre as ilhas A e B é:
a) 2,3 km
b) 2,1 km
c) 1,9 km
d) 1,4 km
e) 1,7 km
Ver Resposta
3. (Unifor-CE) Sabe-se que em todo triângulo a medida de cada lado é diretamente proporcional ao seno do ângulo oposto ao lado. Usando essa informação, conclui-se que a medida do lado AB do triângulo representado abaixo é:
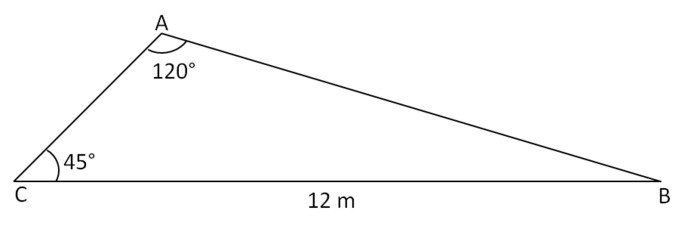
Ver Resposta
Leia mais sobre o tema:
Comentários:
Compilado por Formador: Jose Bernardo Muchanga
Sobre JBM
Esta página foi projetada por JBM para facilitar ao usuário a busca parcial e completa dos conteúdos de várias disciplinas, enriquecendo assim seus estudos.
Gerar pedf desse apontamento inicio


