Triângulo isósceles é um polígono que apresenta três lados, sendo, pelo menos, dois deles congruentes (mesma medida).

O lado com medida diferente é chamado base do triângulo isósceles. O ângulo formado pelos dois lados congruentes é chamado ângulo do vértice.

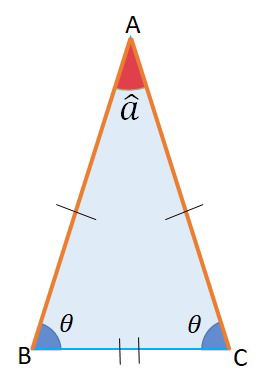
No triângulo isósceles ABC, representado abaixo, os lados  possuem mesma medida. O lado  é a base do triângulo e o ângulo  é o ângulo do vértice. Os ângulos  são os ângulos da base e possuem a mesma medida.

Propriedades dos Triângulos Isósceles

Todo triângulo isósceles apresenta as seguintes propriedades:

• Os ângulos das bases são congruentes (iguais);
• A bissetriz do ângulo do vértice (encontro dos lados iguais), coincide com a altura relativa à base, com a mediana (segmento que liga um vértice ao ponto médio do lado oposto) e a mediatriz (segmento do ponto médio de um lado e perpendicular a este).

Para provar essas propriedades, iremos utilizar um triângulo isósceles ABC. Traçando a bissetriz do ângulo do vértice, formamos os triângulos ABM e ACM, conforme figura abaixo:

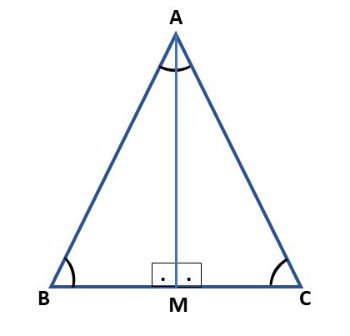
Note que o lado  é comum aos dois triângulos e a bissetriz dividiu o ângulo  em dois ângulos de mesma medida. Além disso, os lados  são congruentes (lados iguais do triângulo isósceles ABC).

Desta forma, temos o caso de congruência de triângulos LAL (lado, ângulo, lado). Concluímos então que os ângulos , da base do triângulo, possuem a mesma medida.

Podemos ainda concluir que, como os triângulos ABM e ACM são congruentes, as medidas de  são iguais.

Portanto,  também é a mediana relativa à base. Além disso,  também é a altura relativa à base, pois forma com a base dois ângulos iguais a 90º.

Fórmula da altura de um triângulo isósceles

No triângulo isósceles, utilizando o teorema de Pitágoras e isolando a altura, encontramos a fórmula:

Onde:

h é a altura;
L é a medida dos lados congruentes;
b é a base.

Área dos Triângulos

Para encontrar a área de um triângulo isósceles usamos a fórmula da área de uma triângulo qualquer:

Onde:

A: área
b: medida da base
h: medida da altura relativa à base

Exemplo:

Qual o valor da área de um triângulo isósceles que apresenta lados com medidas iguais a 10 cm, 10 cm e 12 cm?

A base do triângulo mede 12 cm, contudo, não temos a medida da altura. Entretanto, sabemos que ela coincide com a mediana. Desta forma a altura irá dividir a base em dois segmentos iguais, ou seja 12:2 = 6.

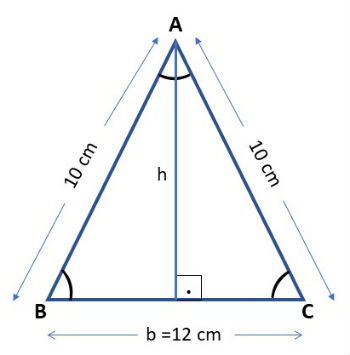
Para encontrar a altura iremos usar o teorema de Pitágoras:

102 = 62 + h2
h2 = 100 - 36
h2 = 64
h = 8 cm

Agora, podemos calcular a área:

Veja também: Exercícios sobre Teorema de Pitágoras (resolvidos e comentados)

Eixo de Simetria

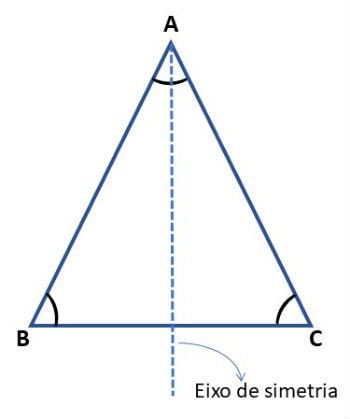
O eixo de simetria de uma figura é uma reta que a divide em duas outras figuras idênticas e que quando dobramos pelo eixo de simetria, essas figuras se sobrepõem perfeitamente.

Os triângulos isósceles apresentam apenas 1 eixo de simetria, que é a reta que divide o ângulo do vértice em dois ângulos iguais (bissetriz).

Baricentro, circuncentro, ortocentro e incentro no triângulo isósceles

Estes pontos estão localizados no eixo de simetria.

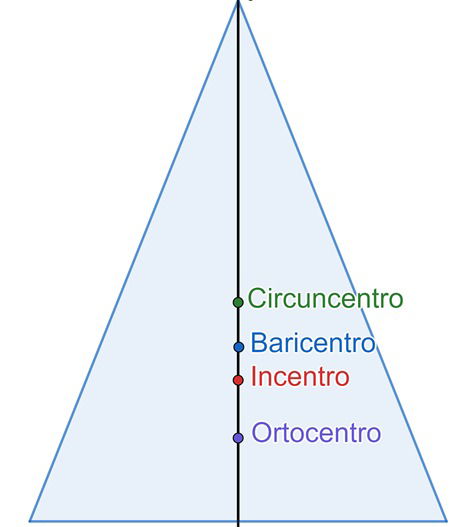
Circuncentro é o ponto de cruzamento entre as três mediatrizes.

Baricentro é o ponto de cruzamento entre as três medianas.

Incentro é o ponto de cruzamento entre as três bissetrizes.

Ortocentro é o ponto de cruzamento entre as três alturas.

Classificação dos Triângulos

Além dos triângulos isósceles, temos ainda os triângulos equiláteros e escalenos. Essa classificação leva em consideração os lados que formam o triângulo.

Assim, o triângulo equilátero é aquele que possui três lados com mesma medida e o escaleno todos os lados apresentam medidas diferentes.

Remover anúncios

Podemos ainda classificar os triângulos em relação aos ângulos internos. O triângulo será acutângulo quando a medida dos ângulos internos for menor que 90º.

Quando o triângulo apresentar um ângulo reto (igual a 90º) será classificado como triângulo retângulo e obtusângulo quanto tiver um ângulo maior que 90º.

Para estudar mais sobre esse conteúdo, leia também:

• Triângulo: tudo sobre este polígono
• Exercícios de Trigonometria
• Área do Triângulo