Disciplina: Matemática, Apontamentos nas Disciplinas básicas (gerais) e essenciais
Apontamentos do Tema: Retas paralelas: o que são, cortadas por uma transversal e exercícios
Retas paralelas: o que são, cortadas por uma transversal e exercícios
Duas retas distintas são paralelas quando possuem a mesma inclinação, ou seja, possuem o mesmo coeficiente angular. Além disso, a distância entre elas é sempre a mesma e não possuem pontos em comum.
As retas paralelas não se cruzam. Na figura abaixo representamos as retas paralelas r e s.
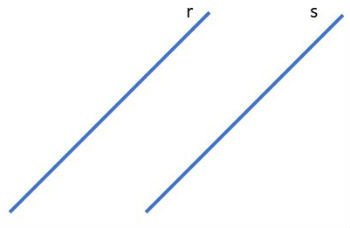
Retas paralelas (r // s)
Diferente das retas paralelas, as retas concorrentes se cruzam em um único ponto.
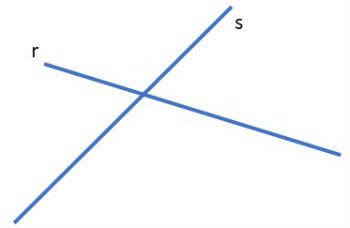
Retas concorrentes
Se duas retas se cruzam em um único ponto e o ângulo formado entre elas no cruzamento for igual a 90º, as retas são chamadas de perpendiculares.
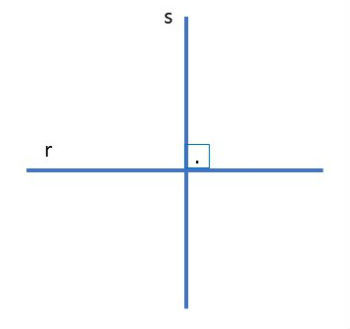
Retas perpendiculares
Para saber mais, leia também:
Retas paralelas cortadas por uma transversal
Uma reta é transversal a outra se possuem apenas um ponto em comum.
Duas retas paralelas r e s, se forem cortadas por uma reta t, transversal a ambas, formará ângulos como representados na imagem abaixo.
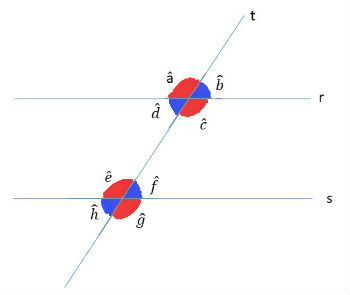
Na figura, os ângulos que apresentam a mesma cor são congruentes, ou seja, possuem mesma medida. Dois ângulos de cores diferentes são suplementares, ou seja, somam 180º.
Por exemplo, os ângulos a e c apresentam mesma medida e a soma dos ângulos f e g é igual a 180º.
Os pares de ângulos recebem nomes conforme a posição que ocupam em relação às retas paralelas e a reta transversal. Sendo assim, os ângulos podem ser:
- Correspondentes
- Alternos
- Colaterais
Ângulos correspondentes
Dois ângulos que ocupam a mesma posição nas retas paralelas são chamados de correspondentes. Eles apresentam a mesma medida (ângulos congruentes).
Os pares de ângulos com a mesma cor representados abaixo são correspondentes.
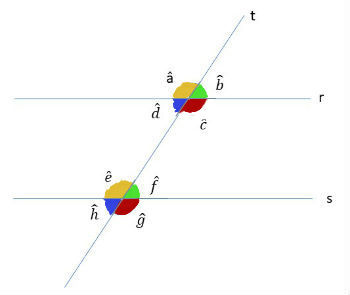
Na figura, os ângulos correspondentes são:
- a e e
- b e f
- c e g
- d e h
Ângulos Alternos
Os pares de ângulos em lados opostos da reta transversal são chamados de alternos. Esses ângulos também são congruentes.
Os ângulos alternos podem ser internos, quando estão entre as retas paralelas e externos, quando estão fora das retas paralelas.
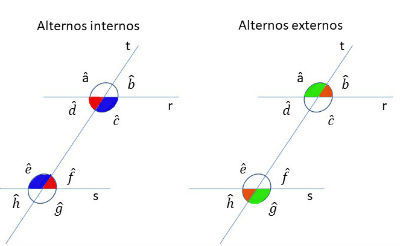
Na figura, os ângulos alternos internos são:
- c e e
- d e f
Os ângulos alternos externos são:
- a e g
- b e h
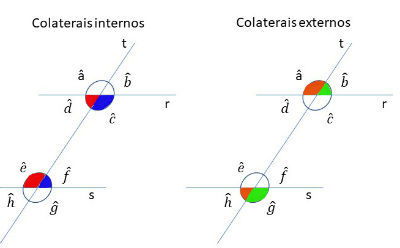
Ângulos colaterais
São os pares de ângulos que estão do mesmo lado da reta transversal. Os ângulos colaterais são suplementares (somam 180º). Também podem ser internos ou externos.
Ainda com dúvidas? Pergunta ao Ajudante IA do Toda Matéria
Palavras: 0/900
Utilizações: 0/5
Resolver
Insira ou cole sua questão (Ctrl + V). Depois, aperte Resolver.
Colar texto
ou
Inserir imagem
Na figura, os ângulos colaterais internos são:
- d e e
- c e f
Os ângulos colaterais externos são:
- a e h
- b e g
Teorema de Tales
Num mesmo plano, um feixe de retas paralelas determinam, em duas retas transversais, segmentos de retas proporcionais.
Exemplo
Os pontos A, A´, B, B´, C, C´ foram obtidos pelo cruzamento das retas paralelas r, s e q com as retas transversais t e v.
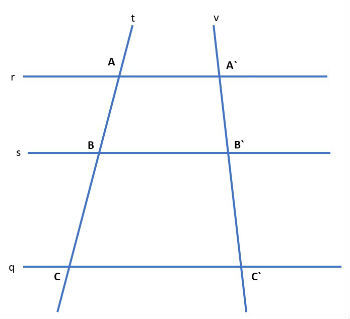
Segundo o teorema de Tales, teremos a seguinte relação:
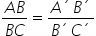
Exercícios resolvidos sobre retas paralelas
Exercício 1
Observando os ângulos entre as retas paralelas e a reta transversal, determine os ângulos indicados na figura:
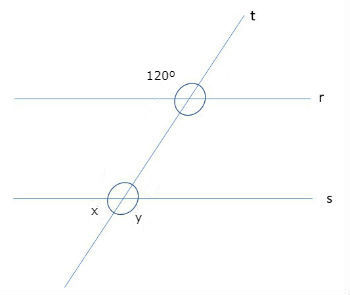
Ver Resposta
Exercício 2
Dada a figura abaixo, encontre o valor do ângulo assinalado, sabendo que as retas r e s são paralelas.
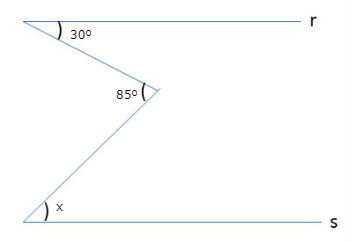
Ver Resposta
Exercício 3
Determine o valor de x na figura abaixo:
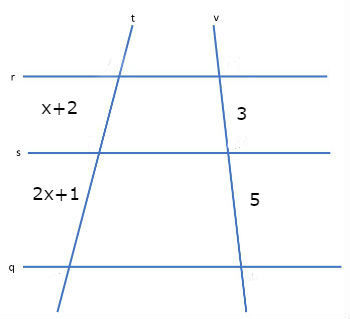
Comentários:
Compilado por Formador: Jose Bernardo Muchanga
Sobre JBM
Esta página foi projetada por JBM para facilitar ao usuário a busca parcial e completa dos conteúdos de várias disciplinas, enriquecendo assim seus estudos.
Gerar pedf desse apontamento inicio