Ângulos Complementares são ângulos que juntos somam 90º. Em um ângulo reto dividido em duas partes, cada uma delas representa um complemento da outra.

Na imagem abaixo, o ângulo AÔC (de 60º) complementa o ângulo CÔB (de 30º). Ao mesmo tempo acontece o inverso, ou seja, o ângulo CÔB complementa o ângulo AÔC.

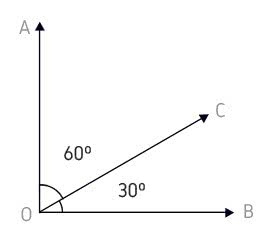
AÔC + CÔB = 90º

Como Calcular?

Para calcular a medida de um ângulo complementar, subtraímos 90º pelo seu complemento:

A + B = 90º
A = 90º - B
B = 90º - A

Exemplos:

1. Calcule o ângulo complementar sabendo que um deles tem 37º.

A + B = 90º
37º + B = 90º
B = 90 - 37º
B = 53º

2. Os ângulos A e B são complementares. Sabendo que A = 60º, indique quanto mede o ângulo B.

A + B = 90º
60º + B = 90º
B = 90º - 60º
B = 30º

Ainda com dúvidas? Pergunta ao Ajudante IA do Toda Matéria

Palavras: 0/900

Utilizações: 0/5

Resolver

Insira ou cole sua questão (Ctrl + V). Depois, aperte Resolver.

Colar texto

ou

Inserir imagem

Ângulos Suplementares e Replementares

Enquanto a soma dos ângulos complementares é igual a 90º, a soma dos ângulos suplementares é igual a 180º.

Os ângulos replementares, por sua vez, são aqueles cuja soma é igual a 360º.

E o que são Ângulos Adjacentes?

Ângulos adjacentes são aqueles que possuem um lado em comum e não possuem pontos internos comuns. Os ângulos adjacentes podem ser complementares. Isso acontece quando esses ângulos juntos medem 90º.

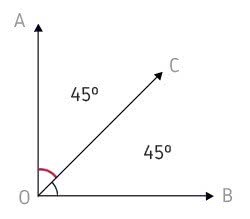
AÔC + CÔB são Ângulos Adjacentes Complementares

Leia também

• Ângulos
• Triângulo Retângulo
• Ângulos Notáveis
• Bissetriz

Exercícios

1. Calcule o complemento do ângulo de 53º.

Ver Resposta

2. Indique a medida dos ângulos complementares tal que um é o triplo do outro.

Ver Resposta

3. Dois ângulos são adjacentes complementares. Sabendo que a medida do maior ângulo é de 47°, qual é a medida do menor ângulo?